§2.1
导数的概念
一、从两个例子来谈导数的概念
变速直线运动物体的速度,是物理上隶属于运动学范畴的问题;平面曲线在一点的切线之斜率,则是一个几何问题。尽管这两个问题有很大的区别,但它们却与一个重要的数学概念
—— 导数有十分密切的关系。

设动点于时刻![]() 在直线上所处的位置为
在直线上所处的位置为![]() ,于是
,于是![]() ,称此函数为位置函数。该如何定义动点在某一时刻的瞬时速度呢?
,称此函数为位置函数。该如何定义动点在某一时刻的瞬时速度呢?
考虑从![]() 到
到![]() 这一时间间隔,质点从位置
这一时间间隔,质点从位置![]() 移动到
移动到![]() ,其质点运动的平均速度为:
,其质点运动的平均速度为:
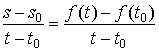
当时间间隔较短时,此比值可近似地看作质点在时刻![]() 的速度。要精确地确定质点在时刻
的速度。要精确地确定质点在时刻![]() 的速度,只需令
的速度,只需令![]() ,对上述表达式取极限,如果这个极限存在,记它为
,对上述表达式取极限,如果这个极限存在,记它为![]()
即: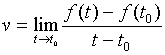 (1)
(1)
此时,极限值![]() 就是质点在时刻
就是质点在时刻![]() 的(瞬时)速度。
的(瞬时)速度。

用matlab摸拟曲线 ![]() 在点
在点![]() 处的割线转动,最终生成曲线在该点的切线,程序为gs201.m。
处的割线转动,最终生成曲线在该点的切线,程序为gs201.m。
设曲线![]() 是函数
是函数![]() 的图形,现讨论
的图形,现讨论![]() 上一点
上一点![]() 处的切线问题。另取
处的切线问题。另取![]() 上一点
上一点![]() ,于是割线
,于是割线![]() 的斜率为
的斜率为
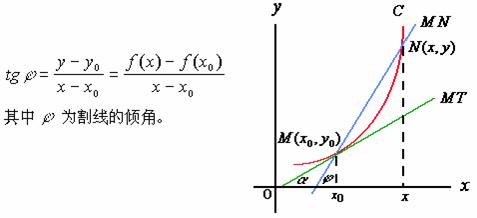
当点![]() 沿
沿![]() 趋于
趋于![]() 时,
时,![]() ,如果上式极限存在,设为
,如果上式极限存在,设为![]() ,即:
,即:
![]() (2)
(2)
![]() 就是割线斜率的极限,也就是切线的斜率。从图上可看出,
就是割线斜率的极限,也就是切线的斜率。从图上可看出,![]() ,且
,且![]() 是切线的倾角。
是切线的倾角。
二、导数定义
变速直线运动的速度和切线的斜率都归结为求如下极限
![]()
这里![]() 和
和![]() 分别是自变量的增量和函数的增量,即:
分别是自变量的增量和函数的增量,即:
![]() ,
, ![]()
而![]() 等价于
等价于![]() ,上述极限可改写成新形式:
,上述极限可改写成新形式:
![]()
由于这类极限在工程技术与自然科学领域里经常遇到,因此,我们有必要对这类特殊形式的极限问题给出一个专门的定义。
1、导数定义
设函数![]() 在点
在点![]() 的某个邻域内有定义,当自变量
的某个邻域内有定义,当自变量![]() 在
在![]() 处取得增量
处取得增量![]() (点
(点![]() 仍在该邻域内)时,函数取得增量
仍在该邻域内)时,函数取得增量
![]()
如果![]() 与
与![]() 之比当
之比当![]() 时的极限存在,则称函数
时的极限存在,则称函数![]() 在
在![]() 处可导,并称这个极限值为函数
处可导,并称这个极限值为函数![]() 在
在![]() 处的导数。记作:
处的导数。记作:![]()
![]() (3)
(3)
也可记作:![]()
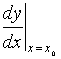
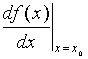
显然,表达式(3)可改写成如下等价的形式:
![]()
或 ![]()
下面我们约定几种说法:
(1)、函数![]() 在点
在点![]() 处可导时,也称
处可导时,也称![]() 在点
在点![]() 具有导数或导数存在。
具有导数或导数存在。
(2)、如果极限(3)不存在,称函数![]() 在点
在点![]() 处不可导。
处不可导。
(3)、若![]() 时,
时,![]() ,则函数
,则函数![]() 在
在![]() 处是不可导的。但为了描述函数的这一特殊性态,我们宁愿称函数在
处是不可导的。但为了描述函数的这一特殊性态,我们宁愿称函数在![]() 处的导数为无穷大。并赋予它记号:
处的导数为无穷大。并赋予它记号:![]() 。
。
2、导函数
如果函数![]() 在开区间
在开区间![]() 内的每一点都可导,称函数
内的每一点都可导,称函数![]() )在开区间
)在开区间![]() 上可导。这时,对任意
上可导。这时,对任意![]() ,都对应着
,都对应着![]() 的一个确定的导数值,这样就构成了一个新的函数,我们此函数为导函数。记作:
的一个确定的导数值,这样就构成了一个新的函数,我们此函数为导函数。记作:![]()
导函数的定义只需将(3)式中的![]() 换成
换成![]() 即可:
即可:
![]()
注意:
虽然![]() 在开区间
在开区间![]() 上任意取值,一经取定,对于极限过程
上任意取值,一经取定,对于极限过程![]() 来说,它应被视为常量。
来说,它应被视为常量。
很明显,函数![]() 在点
在点![]() 处的导数
处的导数![]() ,就是它的导函数
,就是它的导函数![]() 在
在![]() 处的函数值。即:
处的函数值。即:![]()
三、求导举例
【例1】利用导数定义,证明下列导数公式
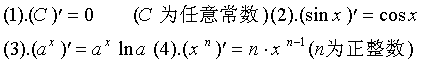
证明:
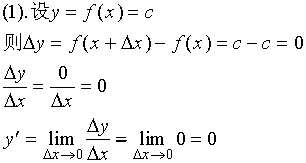
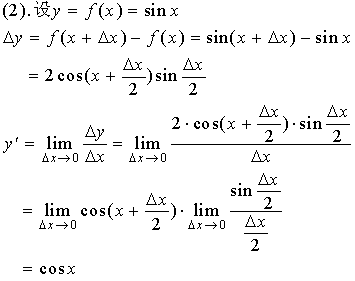
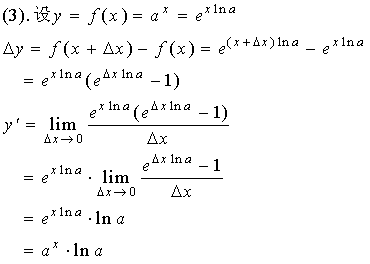
特款:当![]() 时,
时,![]() ,该表达式的简明,获益于自然对数。
,该表达式的简明,获益于自然对数。
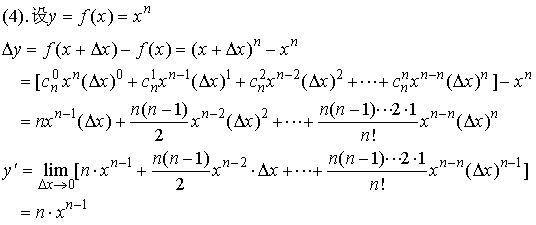
【例2】试证明函数 ![]() 在
在 ![]() 处不可导。
处不可导。
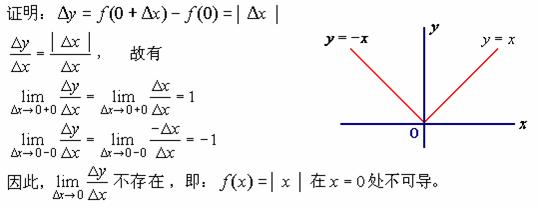
由此例,我们可引入左、右导数的概念。
如果极限
![]()
存在,
则称此极限值为函数在处的左导数(右导数)。记作:
![]()
![]()
利用函数极限与其左、右极限的关系,很容易想到下述结论:
函数![]() 在点
在点![]() 处可导的充要条件是左、右导数
处可导的充要条件是左、右导数![]() 、
、![]() 存在且相等。
存在且相等。
现在, 我们可以给出函数在闭区间![]() 上可导的定义:
上可导的定义:
![]() 在开区间
在开区间![]() 内可导, 且
内可导, 且 ![]() 及
及 ![]() 都存在。
都存在。
四、导数的几何意义
由切线问题的讨论可知:

注记:
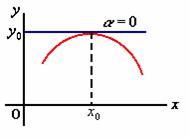
(1)、当![]() 时,
时,![]() ,
,![]() ,
,![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() 。
。
切线平行于![]() 轴,即曲线在
轴,即曲线在![]() 点具有水平切线,其法线方程为
点具有水平切线,其法线方程为![]() 。
。
(2)、若![]() ,
,![]() ,
,![]() ,曲线在
,曲线在![]() 的切线垂直于
的切线垂直于![]() 轴,故切线方程为
轴,故切线方程为 ![]() ,法线方程自然是
,法线方程自然是![]() 。
。
五、函数的可导性与连续性的关系
【命题】若![]() 在
在![]() 处可导,则
处可导,则![]() 在
在![]() 处连续;
处连续;
反之,却不一定成立。
证明:
![]()
故 ![]() (
( ![]() ,当
,当 ![]() 时)
时)
![]()
从而 ![]()
故函数![]() 在
在![]() 处连续。
处连续。
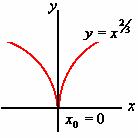
反过来,结论不真。例如:![]() 在
在![]() 处连续,但不可导。
处连续,但不可导。